| The Atomic Nucleus |
Above left: an oblate (flattened spheroid) nucleus with a negative quadrupole moment. Above centre: a
prolate nucleus with a positive quadrupole moment, and above right: a spherical nucleus (with zero
electric quadrupole moment). Click thumbnails to enlarge.
prolate nucleus with a positive quadrupole moment, and above right: a spherical nucleus (with zero
electric quadrupole moment). Click thumbnails to enlarge.
What is the atomic nucleus and how large and dense is it?
At the centre of every atom is the atomic nucleus. The nucleus consists of particles called protons and
neutrons (collectively called nucleons) and contains almost all of the atom's mass, but is extremely tiny, with a
diameter of about 10^-15 metres (0.000 000 000 000 001 m) or one femtometre (one fm = 10^-15 m). This is
only about one hundred thousandth the diameter of an atom (which is about 10^-10 m or 0.1 nanometre or 1
angstrom). Considering that most of the mass of an atom is contained in the nucleus of the atom, and yet the
nucleus is so tiny, means that the nuclear material is extremely dense!
Consider, for example, a one kilogram bar of gold, which is about 10 cm by 2.5 cm by 2 cm, then all the
atomic nuclei put together would combine to give a cube of volume of about one thousandth of a millimetre
across and yet this microscopic cube would contain more than 99.99% of the gold bar's mass!
A teaspoonful of nuclear matter would weigh some 5 x 10^9 tonnes (5 billion tonnes!).
We cannot relate to such dense matter with our everyday experiences. Additionally this matter is so tiny that
the laws of quantum physics apply, and these laws are very different to those we are familiar with in our large
world. Nuclei are very strange objects indeed!
As examples, the simplest nucleus is that of hydrogen, consisting of a single proton (and zero, one or two
neutrons) whilst that of uranium is one of the heaviest naturally occurring nuclei and contains 92 protons and
between about 141 and 146 neutrons. Atoms whose nuclei have the same number of protons (Z) belong to
the same element, but those with differing neutrons (N) are different isotopes of the element. Very heavy
nuclei, such as those of uranium, are unstable and prone to decay into lighter and more stable nuclei by
releasing radiation. Unstable isotopes are called radioactive isotopes or radioisotopes.
The proton carries one unit of positive electric charge, whilst the neutron carries no net electric charge
(recall that the electron carries one unit of negative electric charge, and that the flow of electrons down an
electric wire carries the electricity).
Given the strangeness of the nuclear world, it is little wonder that physicists on Earth have no totally reliable
model to explain nuclear properties. However, there are several models which accurately describe and
predict several nuclear properties, and a combination of some of these models works pretty well.
Models of the Atomic Nucleus
The Liquid Drop Model
The nucleus can be modelled as a tiny drop of incompressible ultradense liquid. Just as a drop of water has
a surface film of water under tension surrounding it, so does the nucleus. This model predicts that the
nucleus will be spherical, and it accurately describes the masses of many nuclei and correctly predicts that
nuclei are more stable if they have an equal number of protons and neutrons (Z=N). However, the liquid drop
model does not accurately predict the existence of magic numbers.
Magic numbers are certain precise numbers of protons and neutrons that make nuclei particularly stable.
These magic numbers are:
Z and/or N = 2, 8, 20, 28, 50, 82, 126.
For example, nuclei with Z = 20 are particularly stable, for example. These nuclei are all isotopes of calcium,
5 of which are extremely stable and one fairly stable. Helium-4, with 2 protons (Z = 2) and 2 neutrons (N = 2)
is a very stable nucleus. However, nuclei with one neutron more than a magic number, for example
oxygen-17 (with 8 protons and 9 neutrons) is a neutron-emitter, emitting neutron radiation to remove its
access neutron and come back down to the more stable oxygen-16 with 8 protons and 8 neutrons. The liquid
drop model also predicts the average nucleon binding energy, which is equivalent to the energy required to
pull a proton or neutron away from the nucleus.
The Shell Model
If you have read the sections on atoms and electron shells (or otherwise know about these things) then you
may have noticed the similarity between the magic numbers and the complete shells of electrons, which are
also stable, and consist of the electron numbers 2, 8, 20, 28, 50, 82, 126. These electron numbers are
particularly stable and give rise to the noble gases which are chemically very non-reactive, these noble
gases are helium, He (2 electrons), Neon, Ne (10 electrons in two subshells of 2 and 8), Argon, Ar (18
electrons with 8 in its outermost subshell) and Krypton, Kr, Xenon, Xe, Radon, Rn also with 8 electrons in
their outermost sub-shells. Argon, for example, occurs in the air as a gas consisting of particles that are
single atoms, since the atoms will not react with anything else. Burn materials in air and they react with the
oxygen and possibly the nitrogen and carbon dioxide, but never with the argon.
Using the electron shells as an analogy, the shell model of the nucleus constructs a nucleus from protons
and neutrons that occupy different energy levels, with several energy levels or shells. There are also
subshells (s, p, d and f subshells as for electrons, but also the higher g and h subshells). Thus, the energy
levels of the nucleons are quantised - meaning that each nucleon can have only one of a spectrum of
discrete energy values with only certain values allowed.
The shell model of the nucleus accurately predicts the existence of the observed magic numbers. It also
predicts how the magnetic fields generated by moving protons affects the energy levels of the protons
(protons carry positive electric charge and moving charges generate magnetic fields). The shell model also
predicts the spin (a measure of rotation or angular momentum) of most nuclei in their ground states. It also
predicts the existence of excited states - when one or more nucleons absorb energy of the right amount (for
example from X-rays) then they can jump to higher energy levels and the nucleus is said to be excited or in
an excited state. Eventually the nucleons radiate X-rays and return back down to their ground states
(non-excited states).
At the centre of every atom is the atomic nucleus. The nucleus consists of particles called protons and
neutrons (collectively called nucleons) and contains almost all of the atom's mass, but is extremely tiny, with a
diameter of about 10^-15 metres (0.000 000 000 000 001 m) or one femtometre (one fm = 10^-15 m). This is
only about one hundred thousandth the diameter of an atom (which is about 10^-10 m or 0.1 nanometre or 1
angstrom). Considering that most of the mass of an atom is contained in the nucleus of the atom, and yet the
nucleus is so tiny, means that the nuclear material is extremely dense!
Consider, for example, a one kilogram bar of gold, which is about 10 cm by 2.5 cm by 2 cm, then all the
atomic nuclei put together would combine to give a cube of volume of about one thousandth of a millimetre
across and yet this microscopic cube would contain more than 99.99% of the gold bar's mass!
A teaspoonful of nuclear matter would weigh some 5 x 10^9 tonnes (5 billion tonnes!).
We cannot relate to such dense matter with our everyday experiences. Additionally this matter is so tiny that
the laws of quantum physics apply, and these laws are very different to those we are familiar with in our large
world. Nuclei are very strange objects indeed!
As examples, the simplest nucleus is that of hydrogen, consisting of a single proton (and zero, one or two
neutrons) whilst that of uranium is one of the heaviest naturally occurring nuclei and contains 92 protons and
between about 141 and 146 neutrons. Atoms whose nuclei have the same number of protons (Z) belong to
the same element, but those with differing neutrons (N) are different isotopes of the element. Very heavy
nuclei, such as those of uranium, are unstable and prone to decay into lighter and more stable nuclei by
releasing radiation. Unstable isotopes are called radioactive isotopes or radioisotopes.
The proton carries one unit of positive electric charge, whilst the neutron carries no net electric charge
(recall that the electron carries one unit of negative electric charge, and that the flow of electrons down an
electric wire carries the electricity).
Given the strangeness of the nuclear world, it is little wonder that physicists on Earth have no totally reliable
model to explain nuclear properties. However, there are several models which accurately describe and
predict several nuclear properties, and a combination of some of these models works pretty well.
Models of the Atomic Nucleus
The Liquid Drop Model
The nucleus can be modelled as a tiny drop of incompressible ultradense liquid. Just as a drop of water has
a surface film of water under tension surrounding it, so does the nucleus. This model predicts that the
nucleus will be spherical, and it accurately describes the masses of many nuclei and correctly predicts that
nuclei are more stable if they have an equal number of protons and neutrons (Z=N). However, the liquid drop
model does not accurately predict the existence of magic numbers.
Magic numbers are certain precise numbers of protons and neutrons that make nuclei particularly stable.
These magic numbers are:
Z and/or N = 2, 8, 20, 28, 50, 82, 126.
For example, nuclei with Z = 20 are particularly stable, for example. These nuclei are all isotopes of calcium,
5 of which are extremely stable and one fairly stable. Helium-4, with 2 protons (Z = 2) and 2 neutrons (N = 2)
is a very stable nucleus. However, nuclei with one neutron more than a magic number, for example
oxygen-17 (with 8 protons and 9 neutrons) is a neutron-emitter, emitting neutron radiation to remove its
access neutron and come back down to the more stable oxygen-16 with 8 protons and 8 neutrons. The liquid
drop model also predicts the average nucleon binding energy, which is equivalent to the energy required to
pull a proton or neutron away from the nucleus.
The Shell Model
If you have read the sections on atoms and electron shells (or otherwise know about these things) then you
may have noticed the similarity between the magic numbers and the complete shells of electrons, which are
also stable, and consist of the electron numbers 2, 8, 20, 28, 50, 82, 126. These electron numbers are
particularly stable and give rise to the noble gases which are chemically very non-reactive, these noble
gases are helium, He (2 electrons), Neon, Ne (10 electrons in two subshells of 2 and 8), Argon, Ar (18
electrons with 8 in its outermost subshell) and Krypton, Kr, Xenon, Xe, Radon, Rn also with 8 electrons in
their outermost sub-shells. Argon, for example, occurs in the air as a gas consisting of particles that are
single atoms, since the atoms will not react with anything else. Burn materials in air and they react with the
oxygen and possibly the nitrogen and carbon dioxide, but never with the argon.
Using the electron shells as an analogy, the shell model of the nucleus constructs a nucleus from protons
and neutrons that occupy different energy levels, with several energy levels or shells. There are also
subshells (s, p, d and f subshells as for electrons, but also the higher g and h subshells). Thus, the energy
levels of the nucleons are quantised - meaning that each nucleon can have only one of a spectrum of
discrete energy values with only certain values allowed.
The shell model of the nucleus accurately predicts the existence of the observed magic numbers. It also
predicts how the magnetic fields generated by moving protons affects the energy levels of the protons
(protons carry positive electric charge and moving charges generate magnetic fields). The shell model also
predicts the spin (a measure of rotation or angular momentum) of most nuclei in their ground states. It also
predicts the existence of excited states - when one or more nucleons absorb energy of the right amount (for
example from X-rays) then they can jump to higher energy levels and the nucleus is said to be excited or in
an excited state. Eventually the nucleons radiate X-rays and return back down to their ground states
(non-excited states).
Above left: a nucleus with a magic number of protons plus one. The extra proton moves in an orbit around
the nuclear equator (loosely speaking - nucleons, like electrons, do not really move in precise orbits, but this
is one of the easiest ways to imagine them!) forming an equatorial bulge. Above right: a nucleus with a magic
number of protons minus one. The 'proton hole' forms an equatorial groove. In reality nuclei, like electron
shells, are complex waves that determine the probability distribution of electric charge, which is approximately
spherical or ellipsoidal. See the description of atoms as waves for a better picture of this in the electron case.
the nuclear equator (loosely speaking - nucleons, like electrons, do not really move in precise orbits, but this
is one of the easiest ways to imagine them!) forming an equatorial bulge. Above right: a nucleus with a magic
number of protons minus one. The 'proton hole' forms an equatorial groove. In reality nuclei, like electron
shells, are complex waves that determine the probability distribution of electric charge, which is approximately
spherical or ellipsoidal. See the description of atoms as waves for a better picture of this in the electron case.
The Fermi Gas Model
There are two fundamental types of particles, bosons and fermions. Bosons include photons, particles of
light, whilst fermions include electrons, protons and neutrons. Bosons have the unusual property that many
bosons can be in the same physical state at once. Fermions, however, cannot coexist in the same state,
which means that they must have some distinguishing feature, for example, two protons in the same nucleus
must occupy different orbits (energy levels) or spin in opposite directions (counterclockwise and clockwise).
This means that most of the protons and neutrons can move about in the nucleus without colliding with one
another (since they occupy different 'orbits') - the so-called Pauli exclusion principle - a fermion in one state
excludes other fermions from entering that same state (e.g. orbit). The 'state' of a system is a total
description of a system, in terms of its energy and motion, and is unique for fermions, whilst several bosons
can be in the same state at once.
The Fermi gas model models the nucleus as a gas of fermions (a gas of protons and a gas of neutrons)
moving in different states and thereby avoiding collisions most of the time. This is essential, since the
nucleus is so enormously dense and the nucleons move so fast, that if they were to collide too much the
nucleus would blast itself apart! Thus, the Fermi gas model explains why almost all of the nucleons that
compose a nucleus can move freely within the nucleus if it is in its ground state. (In an excited state, the
nucleus may indeed fly apart, as happens in nuclear fission).
The Collective Model
All these models explain some nuclear properties, but no one model explains them all! The collective model
attempts to do this as best as possible by combining features of the liquid drop model and the shell model. It
successfully predicts that some nuclei have a magnetic dipole moment. A bar magnet is a magnetic dipole,
meaning that it has two magnetic poles (north and south) - place two bar magnets together with their north
poles facing one another, or with their south poles facing one another, and they repel one another. Place
them together with their north and south poles facing and they attract one another (like poles repel, opposite
poles attract). Moving electric charges generate magnetic fields, and since the protons make the nucleus
positively charged, as the nucleus spins it generates a magnetic dipole (we say that the nucleus has a
magnetic dipole moment) and so has one magnetic north pole and one magnetic south pole.
A nucleus also has an electric moment, but instead of two electric poles, many nuclei have four, and so it is
said to have an electric quadrupole moment. This tells us that the nucleus consist of an ellipsoid (rugby ball
shape) of electric charge - it is elongated. When a nucleus has no electric quadrupole moment it is perfectly
spherical. Measurements of the electric quadrupole moment tell us, for example, that nuclei with a magic
number of protons plus one, have an equatorial bulge of positive electric charge (as shown in the picture
above). Other nuclei are oblate or ellipsoid (see the introductory pictures at the top of the page).
Nuclear Fission
The electrons orbit the nucleus of an atom because their negative electric charge is attracted to the positive
electric charge of the nucleus (due to its protons). This electric force is called the Coulomb force. However,
like electric charges repel (we have a repulsive Coulomb force), so what stops the positively charged protons
that are crammed so densely into the nucleus from flying apart? Part of the answer is due to the neutrons.
Neutrons have zero net charge and so serve to screen the protons from one another's Coulomb repulsion.
However, this alone is insufficient. It turns out that nucleons in the nucleus are held together by a force that is
much stronger than the Coulomb force and is attractive, pulling the nucleons together. This force is the
nuclear force. This force is so strong, that if a nucleus is split into two smaller fragments, reducing the strong
nuclear force between them, then tremendous amounts of energy are released.
For most stable nuclei, the amount of energy put in to break the nucleus apart is so great, as to make it not
worth the trouble if you are after lots of energy. However, large nuclei, with lots of nucleons become
increasingly unstable, in part because the huge numbers of protons build up so much Coulomb repulsion
that it is finely balanced by the nuclear force, especially because the nuclear force is very short range,
making it less effective at holding a large nucleus together.
Consider uranium-235 (92 protons and 143 neutrons). This isotope of uranium is unstable and prone to
decay by releasing radiation, it is a radioisotope. If left to its own devices, then the uranium-235 will emit an
alpha particle (alpha radiation) from its nucleus (an alpha particle consists of two protons and two neutrons)
and turn itself into thorium-231 (90 protons and 141 neutrons) which will undergo further radioactive decay,
and so on, until a stable nucleus is reached. Each step in this radioactive decay series releases a relatively
small amount of energy (though still harmful to humans!). If more nuclear energy could be released at once,
then that energy could be better used to generate electricity or to make a nuclear bomb.
It just so happens that if one fires neutrons at uranium-235, then a nucleus may catch one of the neutrons.
This gives the already unstable nucleus too many nucleons and too much energy. The nucleus becomes
excited and possibly vibrates violently, stretching vertically and horizontally in alternate fashion, until it
elongates too much and starts to split apart as the Coulomb repulsion of its protons overcome the
short-range nuclear force when the nucleus elongates. This causes the nucleus to split into two smaller
nuclei - a process called nuclear fission ('splitting the atom'). As the two nuclear fragments move apart, they
escape the strong attractive force between them and the repulsion takes over and they fly apart with
tremendous speed (rather like pulling apart two incredibly strong magnets - you are likely to go flying with
one of them!). In a nuclear reactor, these fragments are stopped by the materials in the reactor, and the
energy of their motion (kinetic energy) is turned into heat. This heat can be used to turn water into steam
and drive turbines to generate electricity. The waste products of nuclear fission reactors also provide useful
radioisotopes for medicine (such as those used for radiotherapy).
The video below shows a nucleus in the process of fission - it has absorbed a neutron and become excited
into strong vibrations until it pulls itself apart. If the video does not display on your Web browser then click the
link below to download it, or look at the selected stills underneath:
There are two fundamental types of particles, bosons and fermions. Bosons include photons, particles of
light, whilst fermions include electrons, protons and neutrons. Bosons have the unusual property that many
bosons can be in the same physical state at once. Fermions, however, cannot coexist in the same state,
which means that they must have some distinguishing feature, for example, two protons in the same nucleus
must occupy different orbits (energy levels) or spin in opposite directions (counterclockwise and clockwise).
This means that most of the protons and neutrons can move about in the nucleus without colliding with one
another (since they occupy different 'orbits') - the so-called Pauli exclusion principle - a fermion in one state
excludes other fermions from entering that same state (e.g. orbit). The 'state' of a system is a total
description of a system, in terms of its energy and motion, and is unique for fermions, whilst several bosons
can be in the same state at once.
The Fermi gas model models the nucleus as a gas of fermions (a gas of protons and a gas of neutrons)
moving in different states and thereby avoiding collisions most of the time. This is essential, since the
nucleus is so enormously dense and the nucleons move so fast, that if they were to collide too much the
nucleus would blast itself apart! Thus, the Fermi gas model explains why almost all of the nucleons that
compose a nucleus can move freely within the nucleus if it is in its ground state. (In an excited state, the
nucleus may indeed fly apart, as happens in nuclear fission).
The Collective Model
All these models explain some nuclear properties, but no one model explains them all! The collective model
attempts to do this as best as possible by combining features of the liquid drop model and the shell model. It
successfully predicts that some nuclei have a magnetic dipole moment. A bar magnet is a magnetic dipole,
meaning that it has two magnetic poles (north and south) - place two bar magnets together with their north
poles facing one another, or with their south poles facing one another, and they repel one another. Place
them together with their north and south poles facing and they attract one another (like poles repel, opposite
poles attract). Moving electric charges generate magnetic fields, and since the protons make the nucleus
positively charged, as the nucleus spins it generates a magnetic dipole (we say that the nucleus has a
magnetic dipole moment) and so has one magnetic north pole and one magnetic south pole.
A nucleus also has an electric moment, but instead of two electric poles, many nuclei have four, and so it is
said to have an electric quadrupole moment. This tells us that the nucleus consist of an ellipsoid (rugby ball
shape) of electric charge - it is elongated. When a nucleus has no electric quadrupole moment it is perfectly
spherical. Measurements of the electric quadrupole moment tell us, for example, that nuclei with a magic
number of protons plus one, have an equatorial bulge of positive electric charge (as shown in the picture
above). Other nuclei are oblate or ellipsoid (see the introductory pictures at the top of the page).
Nuclear Fission
The electrons orbit the nucleus of an atom because their negative electric charge is attracted to the positive
electric charge of the nucleus (due to its protons). This electric force is called the Coulomb force. However,
like electric charges repel (we have a repulsive Coulomb force), so what stops the positively charged protons
that are crammed so densely into the nucleus from flying apart? Part of the answer is due to the neutrons.
Neutrons have zero net charge and so serve to screen the protons from one another's Coulomb repulsion.
However, this alone is insufficient. It turns out that nucleons in the nucleus are held together by a force that is
much stronger than the Coulomb force and is attractive, pulling the nucleons together. This force is the
nuclear force. This force is so strong, that if a nucleus is split into two smaller fragments, reducing the strong
nuclear force between them, then tremendous amounts of energy are released.
For most stable nuclei, the amount of energy put in to break the nucleus apart is so great, as to make it not
worth the trouble if you are after lots of energy. However, large nuclei, with lots of nucleons become
increasingly unstable, in part because the huge numbers of protons build up so much Coulomb repulsion
that it is finely balanced by the nuclear force, especially because the nuclear force is very short range,
making it less effective at holding a large nucleus together.
Consider uranium-235 (92 protons and 143 neutrons). This isotope of uranium is unstable and prone to
decay by releasing radiation, it is a radioisotope. If left to its own devices, then the uranium-235 will emit an
alpha particle (alpha radiation) from its nucleus (an alpha particle consists of two protons and two neutrons)
and turn itself into thorium-231 (90 protons and 141 neutrons) which will undergo further radioactive decay,
and so on, until a stable nucleus is reached. Each step in this radioactive decay series releases a relatively
small amount of energy (though still harmful to humans!). If more nuclear energy could be released at once,
then that energy could be better used to generate electricity or to make a nuclear bomb.
It just so happens that if one fires neutrons at uranium-235, then a nucleus may catch one of the neutrons.
This gives the already unstable nucleus too many nucleons and too much energy. The nucleus becomes
excited and possibly vibrates violently, stretching vertically and horizontally in alternate fashion, until it
elongates too much and starts to split apart as the Coulomb repulsion of its protons overcome the
short-range nuclear force when the nucleus elongates. This causes the nucleus to split into two smaller
nuclei - a process called nuclear fission ('splitting the atom'). As the two nuclear fragments move apart, they
escape the strong attractive force between them and the repulsion takes over and they fly apart with
tremendous speed (rather like pulling apart two incredibly strong magnets - you are likely to go flying with
one of them!). In a nuclear reactor, these fragments are stopped by the materials in the reactor, and the
energy of their motion (kinetic energy) is turned into heat. This heat can be used to turn water into steam
and drive turbines to generate electricity. The waste products of nuclear fission reactors also provide useful
radioisotopes for medicine (such as those used for radiotherapy).
The video below shows a nucleus in the process of fission - it has absorbed a neutron and become excited
into strong vibrations until it pulls itself apart. If the video does not display on your Web browser then click the
link below to download it, or look at the selected stills underneath:
Left: prior to fission, the nucleus has
absorbed a neutron and is vibrating.
absorbed a neutron and is vibrating.
Left: the nucleus elongates until it
starts to pull itself in two, forming a
neck region between the two
separating fragments.
starts to pull itself in two, forming a
neck region between the two
separating fragments.
Left: the two fragments separate as
two smaller nuclei (more often than not
one fragment will be larger than the
other).
two smaller nuclei (more often than not
one fragment will be larger than the
other).
The two nuclear fragments fly apart at
tremendous speeds (like a broken
spring that was very tightly wound!).
tremendous speeds (like a broken
spring that was very tightly wound!).
In addition to splitting in two, a nucleus of uranium releases two or three neutrons. These neutrons fly
off and if they hit other uranium nuclei and become absorbed by them, they may trigger another two
or three uranium nuclei to split. This process continues, rapidly gaining momentum as a chain
reaction. This is what happens in a nuclear explosion. In a nuclear reactor, the aim is to prevent the
chain reaction from running away by controlling it (otherwise a reactor core meltdown will occur!).
Some very heavy nuclei are prone to spontaneous fission - existing in an unstable state and
spontaneously undergoing alpha-decay or nuclear fission. (Alpha decay is really a form of fission in
which a small helium nucleus, or alpha particle, splits away). Other heavy nuclei can only be induced
to undergo fission (induced fission) by bombarding them with high energy particles, such as
neutrons or X-rays. Spontaneous fission is usually asymmetric fission, with one daughter nucleus
being more massive than the other. Induced fission, however, becomes more symmetric as the energy
of the bombarding particles increases until it becomes symmetric fission (as depicted in our
diagrams). Most fission events are binary fission, in which one nucleus splits into two daughter
nuclei. About 0.2 to 0.3% of fission events, however, are ternary fission events, in which three
products are formed, one of them is usually a light nucleus such as an alpha particle.
Heavier stable nuclei have a greater excess of neutrons. This means that the two smaller daughter
nuclei will inherit too many neutrons and so will be unstable. Some neutrons are immediately emitted
(the prompt neutrons) with energies ranging from 1 to 15 MeV. Gamma-rays (high-energy photons)
are also emitted due to rapid charge (proton) rearrangements in the daughter nuclei. The daughter
nuclei (fission fragments) may still be unstable and reduce their neutron number by undergoing
beta-decay, in which a proton transforms into a proton, electron (beta-particle) and electron neutrino.
The electron and neutrino are emitted with high energies.
off and if they hit other uranium nuclei and become absorbed by them, they may trigger another two
or three uranium nuclei to split. This process continues, rapidly gaining momentum as a chain
reaction. This is what happens in a nuclear explosion. In a nuclear reactor, the aim is to prevent the
chain reaction from running away by controlling it (otherwise a reactor core meltdown will occur!).
Some very heavy nuclei are prone to spontaneous fission - existing in an unstable state and
spontaneously undergoing alpha-decay or nuclear fission. (Alpha decay is really a form of fission in
which a small helium nucleus, or alpha particle, splits away). Other heavy nuclei can only be induced
to undergo fission (induced fission) by bombarding them with high energy particles, such as
neutrons or X-rays. Spontaneous fission is usually asymmetric fission, with one daughter nucleus
being more massive than the other. Induced fission, however, becomes more symmetric as the energy
of the bombarding particles increases until it becomes symmetric fission (as depicted in our
diagrams). Most fission events are binary fission, in which one nucleus splits into two daughter
nuclei. About 0.2 to 0.3% of fission events, however, are ternary fission events, in which three
products are formed, one of them is usually a light nucleus such as an alpha particle.
Heavier stable nuclei have a greater excess of neutrons. This means that the two smaller daughter
nuclei will inherit too many neutrons and so will be unstable. Some neutrons are immediately emitted
(the prompt neutrons) with energies ranging from 1 to 15 MeV. Gamma-rays (high-energy photons)
are also emitted due to rapid charge (proton) rearrangements in the daughter nuclei. The daughter
nuclei (fission fragments) may still be unstable and reduce their neutron number by undergoing
beta-decay, in which a proton transforms into a proton, electron (beta-particle) and electron neutrino.
The electron and neutrino are emitted with high energies.


The half-life of fission fragments (the constant time taken for half of them to decay) can vary from less than 1
second to some 10 million years, depending on the isotope. Fission fragments may undergo several
beta-decays in series, until they become stable. Secondary delayed neutrons may also be emitted after a
beta-decay.
Natural uranium consists of 99.27% uranium-238 atoms and 0.72% uranium-235. Slow (i.e. low-energy)
neutron bombardment can induce fission in U-235, but a neutron energy of 1.2 MeV or more is required to
induce fission in U-238. In order to undergo fission or alpha-decay, the system has to move from one energy
state to another. The diagram below illustrates the potential energy well of a nucleus. A potential energy
well represents a force-field and in this case it represents the force-field that holds the nucleons in the
nucleus - this is the nuclear force. This attractive force overcomes the repulsive Coulomb force between the
protons, which tend to repel one-another since they have like (positive) electric charges. Thus, the overall
force-field has to take into account both the nuclear and Coulomb forces. Thinking of a nucleus as a
liquid-drop, the binding nuclear force acts a lot like the forces that bind water molecules together, and
generates surface-tension - an elastic skin, if you like, that pulls the nucleus together should it stretch as its
components attempt to fly apart under Coulomb repulsion. For an unstable nucleus to exist for any
reasonable length of time at all, the nuclear force must ordinarily win against the Coulomb repulsion, albeit
only just. The potential energy well is illustrated below:
second to some 10 million years, depending on the isotope. Fission fragments may undergo several
beta-decays in series, until they become stable. Secondary delayed neutrons may also be emitted after a
beta-decay.
Natural uranium consists of 99.27% uranium-238 atoms and 0.72% uranium-235. Slow (i.e. low-energy)
neutron bombardment can induce fission in U-235, but a neutron energy of 1.2 MeV or more is required to
induce fission in U-238. In order to undergo fission or alpha-decay, the system has to move from one energy
state to another. The diagram below illustrates the potential energy well of a nucleus. A potential energy
well represents a force-field and in this case it represents the force-field that holds the nucleons in the
nucleus - this is the nuclear force. This attractive force overcomes the repulsive Coulomb force between the
protons, which tend to repel one-another since they have like (positive) electric charges. Thus, the overall
force-field has to take into account both the nuclear and Coulomb forces. Thinking of a nucleus as a
liquid-drop, the binding nuclear force acts a lot like the forces that bind water molecules together, and
generates surface-tension - an elastic skin, if you like, that pulls the nucleus together should it stretch as its
components attempt to fly apart under Coulomb repulsion. For an unstable nucleus to exist for any
reasonable length of time at all, the nuclear force must ordinarily win against the Coulomb repulsion, albeit
only just. The potential energy well is illustrated below:
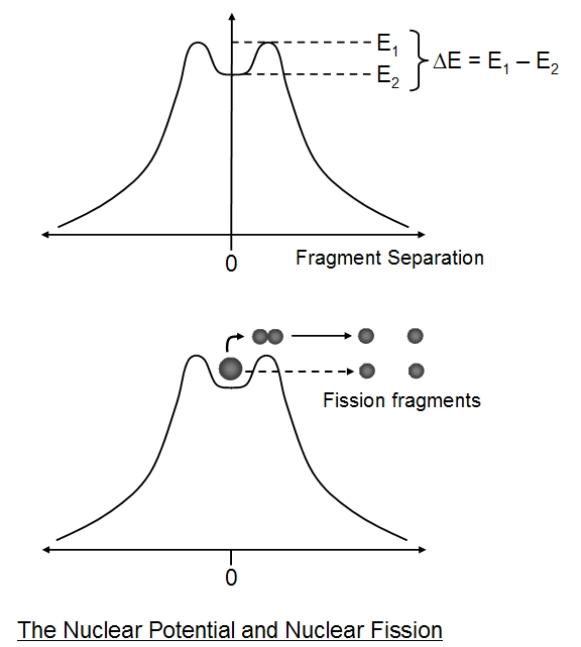
Above: the nuclear potential. You can imagine rotating the curve around the vertical axis to gain a more 3D
perspective in which the nucleus (grey ball) normally sits in the well, which is like a caldera on top of a
mountain (not literally!). If the nucleus gains energy then it moves up the well from the least energy state or
ground state at the bottom of the well. Just like rolling a ball up a hill, if the nucleus gains energy it gets
pushed up the well until, eventually it sits on the rim at the top, at which point the nucleus has its maximum
energy and is about to split in two. The height of the well depends on the isotope. It may roll back down and
become one stable nucleus again, by losing energy, or it may undergo fission, with one fragment leaving the
other nucleus behind in the well. (It isn't quite that simple, of course, each nucleus sits in its own well, but we
can think of our well as being the one for the parent nucleus and larger fragment with the smaller fragment
flying away down the slope.) This is one way in which fission could occur - giving the nucleus enough energy
to clear the rim of the 'caldera'. This would mean giving it enough energy to overcome the surplus of nuclear
force, such that Coulomb repulsion wins and the nucleus flies apart. If this was the only way, then there would
be one definite energy, corresponding to the top of the rim, at which the nucleus suddenly begins fission. In
reality, however, there is a gradual increase in fission probability as the nucleus gains energy and moves
up the well. This can be explained by quantum tunnelling or barrier penetration. There is a small
probability that the nuclear fragment or alpha particles will leave its parent nucleus by passing through the
side of the well (dashed arrow). This is a purely quantum mechanical phenomenon. It would be like bouncing
a ball against a wall and finding that, once in a while the ball mysteriously passes through the wall! This sort
of thing can happen in the atomic and subatomic worlds! The probability of passing through the barrier
increases as the barrier gets smaller. The more energy the nucleus has, the higher it is up the well, where the
'wall' is thinner (and shorter) and the more likely it is that tunnelling will occur.
With uranium, when a neutron hits a U-238 nucleus and sticks to it, a U-239 nucleus is formed, in an excited
state (higher up the well). In fact the nucleus gains some 4.8 MeV (from a slow neutron). The height of the
well (E1 minus E2) is 6 MeV, so the nucleus has not left the well, but tunnelling and hence nuclear fission are
much more likely and may or may not occur. More likely, the nucleus will undergo some other form of
radioactive emission. When a similar neutron binds to a U-235 nucleus, forming a U-236 nucleus, the
incoming neutron is able to pair with a neutron in the U-235 nucleus, since this nucleus has an odd neutron,
but U-238 does not so in the latter case the incoming neutron can not pair. Neutrons and protons like to be in
pairs, so neutron pairing in the U-236 nucleus lowers the energy of the two neutrons and releases the excess
energy to the nucleus which gains not 4.8 MeV, but 6.5 MeV which is enough to clear the well and nuclear
fission occurs immediately.
The stability of nuclei to spontaneous fission and alpha-decay increases if the nucleus has a deeper well.
However, nuclei capable of spontaneous fission seem to exhibit two or more different nuclear states, with the
same numbers of protons and neutrons, but different half-lives. For example, americium-242 (Am-242) has
two such forms, one with a half-life of 14 milliseconds, the other 10 billion years! Thus, one form is stable, the
other is not. this can be explained by a different nuclear potential, illustrated below:
perspective in which the nucleus (grey ball) normally sits in the well, which is like a caldera on top of a
mountain (not literally!). If the nucleus gains energy then it moves up the well from the least energy state or
ground state at the bottom of the well. Just like rolling a ball up a hill, if the nucleus gains energy it gets
pushed up the well until, eventually it sits on the rim at the top, at which point the nucleus has its maximum
energy and is about to split in two. The height of the well depends on the isotope. It may roll back down and
become one stable nucleus again, by losing energy, or it may undergo fission, with one fragment leaving the
other nucleus behind in the well. (It isn't quite that simple, of course, each nucleus sits in its own well, but we
can think of our well as being the one for the parent nucleus and larger fragment with the smaller fragment
flying away down the slope.) This is one way in which fission could occur - giving the nucleus enough energy
to clear the rim of the 'caldera'. This would mean giving it enough energy to overcome the surplus of nuclear
force, such that Coulomb repulsion wins and the nucleus flies apart. If this was the only way, then there would
be one definite energy, corresponding to the top of the rim, at which the nucleus suddenly begins fission. In
reality, however, there is a gradual increase in fission probability as the nucleus gains energy and moves
up the well. This can be explained by quantum tunnelling or barrier penetration. There is a small
probability that the nuclear fragment or alpha particles will leave its parent nucleus by passing through the
side of the well (dashed arrow). This is a purely quantum mechanical phenomenon. It would be like bouncing
a ball against a wall and finding that, once in a while the ball mysteriously passes through the wall! This sort
of thing can happen in the atomic and subatomic worlds! The probability of passing through the barrier
increases as the barrier gets smaller. The more energy the nucleus has, the higher it is up the well, where the
'wall' is thinner (and shorter) and the more likely it is that tunnelling will occur.
With uranium, when a neutron hits a U-238 nucleus and sticks to it, a U-239 nucleus is formed, in an excited
state (higher up the well). In fact the nucleus gains some 4.8 MeV (from a slow neutron). The height of the
well (E1 minus E2) is 6 MeV, so the nucleus has not left the well, but tunnelling and hence nuclear fission are
much more likely and may or may not occur. More likely, the nucleus will undergo some other form of
radioactive emission. When a similar neutron binds to a U-235 nucleus, forming a U-236 nucleus, the
incoming neutron is able to pair with a neutron in the U-235 nucleus, since this nucleus has an odd neutron,
but U-238 does not so in the latter case the incoming neutron can not pair. Neutrons and protons like to be in
pairs, so neutron pairing in the U-236 nucleus lowers the energy of the two neutrons and releases the excess
energy to the nucleus which gains not 4.8 MeV, but 6.5 MeV which is enough to clear the well and nuclear
fission occurs immediately.
The stability of nuclei to spontaneous fission and alpha-decay increases if the nucleus has a deeper well.
However, nuclei capable of spontaneous fission seem to exhibit two or more different nuclear states, with the
same numbers of protons and neutrons, but different half-lives. For example, americium-242 (Am-242) has
two such forms, one with a half-life of 14 milliseconds, the other 10 billion years! Thus, one form is stable, the
other is not. this can be explained by a different nuclear potential, illustrated below:
In this case, we have a smaller well 'outside' of the main well, as if the wells were valleys separated by a high
pass. Within each well some of the energy levels have been drawn as straight lines, which get closer together
towards the top of the well. Since, due to quantum mechanics, the energy of such minute particles as atomic
nuclei is quantised, only certain discrete values are allowed. The nucleus can sit on any of the lines, moving
up to a higher level when it gains energy, moving down when it loses energy, until it reaches the lowest
ground level. Such a double well results from a phenomenon called shape isomerism. If a nucleus is given
energy, it may stretch (either in one direction or another). This stretching changes the height of the energy
levels in the well, and sometimes another metastable set of energy levels results, forming a second well. The
stable americium nucleus sits in the deep central well - it is hard to get anything out of this deep well! The
unstable (or metastable) americium nucleus, however, has a different, more stretched shape (it is a shape
isomer of the stable nucleus) and since this well is shallower, it is easier for fission to occur.
Plutonium-240 (Pu-240) has three shape isomers (a triple well), the one in the shallowest well having a
half-life of only 5 nanoseconds!
pass. Within each well some of the energy levels have been drawn as straight lines, which get closer together
towards the top of the well. Since, due to quantum mechanics, the energy of such minute particles as atomic
nuclei is quantised, only certain discrete values are allowed. The nucleus can sit on any of the lines, moving
up to a higher level when it gains energy, moving down when it loses energy, until it reaches the lowest
ground level. Such a double well results from a phenomenon called shape isomerism. If a nucleus is given
energy, it may stretch (either in one direction or another). This stretching changes the height of the energy
levels in the well, and sometimes another metastable set of energy levels results, forming a second well. The
stable americium nucleus sits in the deep central well - it is hard to get anything out of this deep well! The
unstable (or metastable) americium nucleus, however, has a different, more stretched shape (it is a shape
isomer of the stable nucleus) and since this well is shallower, it is easier for fission to occur.
Plutonium-240 (Pu-240) has three shape isomers (a triple well), the one in the shallowest well having a
half-life of only 5 nanoseconds!

Comment on this article!