| Waves |
Drop a pebble into a pond and you should see something similar to the above - circular waves move out
from the source of the disturbance. In other words, the disturbance spreads out equally in all directions at
the same speed. (You probably wont see as many waves as this from a single pebble!). Notice how the
waves spread out as if trying to fill all the space available to them (in this case the two-dimensional space
of the pond surface).
Just about everything I can think of is either a wave or constructed from waves. Waves are crucial to
understanding quantum phenomena, as we shall see, but first let us focus on the more familiar waves on
water.
Lat's look at a single water wave in profile:
from the source of the disturbance. In other words, the disturbance spreads out equally in all directions at
the same speed. (You probably wont see as many waves as this from a single pebble!). Notice how the
waves spread out as if trying to fill all the space available to them (in this case the two-dimensional space
of the pond surface).
Just about everything I can think of is either a wave or constructed from waves. Waves are crucial to
understanding quantum phenomena, as we shall see, but first let us focus on the more familiar waves on
water.
Lat's look at a single water wave in profile:
Diffraction:
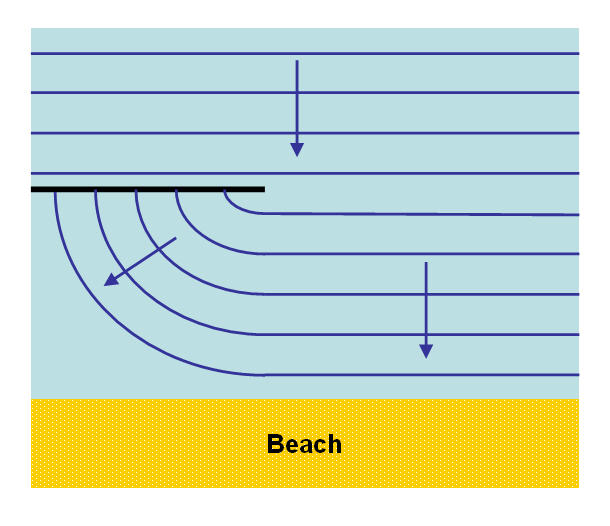
The way in which waves expand into a new area so as to fill all the available space, is called diffraction.
Diffraction is a fundamental property of waves. Diffraction occurs when a wave meets an obstacle in the
water is able to get behind the obstacle, in which case it does so by bending around it. In the picture
below, waves moving toward a beach hit a breakwater (the black line) and curve to fill the space behind it -
this is diffraction of the water waves.
The way in which waves expand into a new area so as to fill all the available space, is called diffraction.
Diffraction is a fundamental property of waves. Diffraction occurs when a wave meets an obstacle in the
water is able to get behind the obstacle, in which case it does so by bending around it. In the picture
below, waves moving toward a beach hit a breakwater (the black line) and curve to fill the space behind it -
this is diffraction of the water waves.
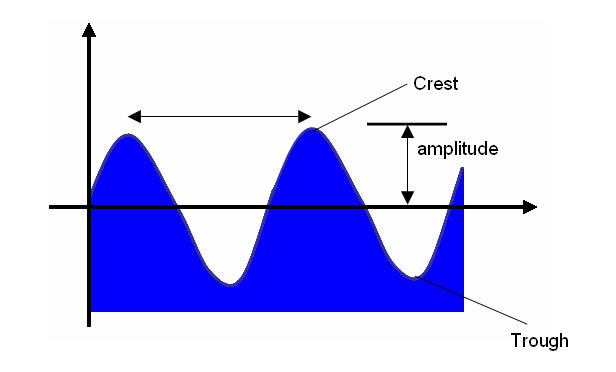
The black horizontal line shows us the level of the water surface when it is at rest. When the wave passes,
the surface undulates, at any instant in time some of the water is displaced upwards and some downwards.
The upward peaks are called the wave crests and the downward deep points are the troughs. The height
of the top of each peak, the crest, from the point at which the water began at rest, is the amplitude of the
wave. Note that the height of the wave is twice the amplitude of the wave, since the height is the distance
from trough to crest. Note also that the volume of water displaced upwards is equal to that displaced
downwards. The distance from crest to neighbouring crest is called the wavelength, and is equal to the
distance from trough to neighbouring trough or between any two similar points on adjacent wave cycles. A
wave cycle is one complete oscillation, from crest to trough and back to crest again. During a cycle the
water essentially bobs up and down and there is no net sideways movement of the water. This can be
seen when one looks at a buoy floating in the water - the buoy bobs up and down, but does not move
sideways, just like the orange buoy in the picture below, which is another wave profile.
the surface undulates, at any instant in time some of the water is displaced upwards and some downwards.
The upward peaks are called the wave crests and the downward deep points are the troughs. The height
of the top of each peak, the crest, from the point at which the water began at rest, is the amplitude of the
wave. Note that the height of the wave is twice the amplitude of the wave, since the height is the distance
from trough to crest. Note also that the volume of water displaced upwards is equal to that displaced
downwards. The distance from crest to neighbouring crest is called the wavelength, and is equal to the
distance from trough to neighbouring trough or between any two similar points on adjacent wave cycles. A
wave cycle is one complete oscillation, from crest to trough and back to crest again. During a cycle the
water essentially bobs up and down and there is no net sideways movement of the water. This can be
seen when one looks at a buoy floating in the water - the buoy bobs up and down, but does not move
sideways, just like the orange buoy in the picture below, which is another wave profile.
Note that what people commonly refer to as a 'wave' is actually a single wave crest, a wave is usually a
train or series of wave crests. If you stand at a particular point, such as on a beach, and count the
number of waves (or strictly wave crests) passing every minute, then this number of wave crests per
minute is a measure of the frequency of the wave. Frequency is usually measured per second, a unit
called the Hertz. For example, if you count 20 waves in one minute, then this is (20 per minute / 60
seconds per minute) 0.3 wave crests per second, a frequency of 0.3 Hertz.
You might be thinking of two objections to the simple picture so far. When you splash hard enough in
the bath, your rubber duck does move sideways a bit, even if you don't 'push' the water toward it. This is
because, in waves which are tall relative to the depth of the water there actually is some sideways
movement of the water. However, in the deep sea, most waves are two shallow compared with the depth
of the sea to cause much sideways movement. Secondly, you might be thinking how you have seen bits
of seaweed slowly bob forwards and backwards as well as up and down when waves pass. This is
because, although there is no net sideways displacement of the water, the water does follow circular
and elliptical orbits, even beneath the surface, as shown below:
train or series of wave crests. If you stand at a particular point, such as on a beach, and count the
number of waves (or strictly wave crests) passing every minute, then this number of wave crests per
minute is a measure of the frequency of the wave. Frequency is usually measured per second, a unit
called the Hertz. For example, if you count 20 waves in one minute, then this is (20 per minute / 60
seconds per minute) 0.3 wave crests per second, a frequency of 0.3 Hertz.
You might be thinking of two objections to the simple picture so far. When you splash hard enough in
the bath, your rubber duck does move sideways a bit, even if you don't 'push' the water toward it. This is
because, in waves which are tall relative to the depth of the water there actually is some sideways
movement of the water. However, in the deep sea, most waves are two shallow compared with the depth
of the sea to cause much sideways movement. Secondly, you might be thinking how you have seen bits
of seaweed slowly bob forwards and backwards as well as up and down when waves pass. This is
because, although there is no net sideways displacement of the water, the water does follow circular
and elliptical orbits, even beneath the surface, as shown below:
In this diagram the wave is moving towards the coast and is passing over the continental shelf in relatively
shallow water. In this shallow water the deeper orbits get vertically squashed into ellipses and these
ellipses get smaller and smaller. Very close to the sand, the water probably simply moves backward and
forward a little bit. This squashing of the orbits does not occur in deeper water, but the orbits do dwindle
with depth - a wave passing over the Atlantic Ocean is not likely to disturb the sea bed over one thousand
metres down below!
Conclusion: water waves are trains of oscillations or undulations in the water's surface, but only the wave
itself and its energy move sideways, there is no net sideways movement of water (unless the
waves are very large).
shallow water. In this shallow water the deeper orbits get vertically squashed into ellipses and these
ellipses get smaller and smaller. Very close to the sand, the water probably simply moves backward and
forward a little bit. This squashing of the orbits does not occur in deeper water, but the orbits do dwindle
with depth - a wave passing over the Atlantic Ocean is not likely to disturb the sea bed over one thousand
metres down below!
Conclusion: water waves are trains of oscillations or undulations in the water's surface, but only the wave
itself and its energy move sideways, there is no net sideways movement of water (unless the
waves are very large).
What drives water waves?
Most water waves are driven by the wind blowing across the surface of the water. Earthquakes, landslide,
under-water volcanic eruptions and other such catastrophic events may also generate water waves. The
longer the open stretch of water that wind can blow across, without hitting a barrier, the stronger and taller
the waves will be. The length of this open surface is called the fetch. The open Ocean has a very long
fetch of a thousand miles or so, whereas on a pond the fetch may be only a few metres, and thus on a
pond the waves will be much weaker and smaller! Once the wind throws water up into a crest, it is gravity
that propagates the wave further - what goes up must come down! This sets the water in motion, as the
wind whips it up and gravity pulls it down. For this reason water waves are often called gravity waves.
(Not are only a few millimetres tall - mere ripples, the effects of surface tension also become important,
and these waves are governed by different physics and mathematical equations and are called capillary
waves. The surface tension is the actual physical tension in the surface film, 'skin' or meniscus of the
water. You may have noticed how tiny things, like insects and leaves, may float on the water without
penetrating its meniscus or skin. This skin is pulled tight across the surface of the water - it is under
tension.
Most water waves are driven by the wind blowing across the surface of the water. Earthquakes, landslide,
under-water volcanic eruptions and other such catastrophic events may also generate water waves. The
longer the open stretch of water that wind can blow across, without hitting a barrier, the stronger and taller
the waves will be. The length of this open surface is called the fetch. The open Ocean has a very long
fetch of a thousand miles or so, whereas on a pond the fetch may be only a few metres, and thus on a
pond the waves will be much weaker and smaller! Once the wind throws water up into a crest, it is gravity
that propagates the wave further - what goes up must come down! This sets the water in motion, as the
wind whips it up and gravity pulls it down. For this reason water waves are often called gravity waves.
(Not are only a few millimetres tall - mere ripples, the effects of surface tension also become important,
and these waves are governed by different physics and mathematical equations and are called capillary
waves. The surface tension is the actual physical tension in the surface film, 'skin' or meniscus of the
water. You may have noticed how tiny things, like insects and leaves, may float on the water without
penetrating its meniscus or skin. This skin is pulled tight across the surface of the water - it is under
tension.
Diffraction also occurs when waves pass through a gap, such as the entrance in the harbour wall in the
picture below. Notice how semicircular waves spread out, or diffract, behind the harbour entrance.
Some coastal tourist destinations like Puerto Penasco Mexico do not have much in the way of harbour
areas. Instead the harbours cater to local fisherman and leave the tourists to one of the many resorts such
as Sonoran Sky Resort Puerto Penasco Mexico.
picture below. Notice how semicircular waves spread out, or diffract, behind the harbour entrance.
Some coastal tourist destinations like Puerto Penasco Mexico do not have much in the way of harbour
areas. Instead the harbours cater to local fisherman and leave the tourists to one of the many resorts such
as Sonoran Sky Resort Puerto Penasco Mexico.
Interference and Superposition of Waves
Another fundamental property of (most) waves is that waves can be added together or subtracted in a
proportional (or linear) manner. You may have noticed how waves can interfere with one another as
they cross over in a pond, changing shape when they coincide (and returning to their original shape as
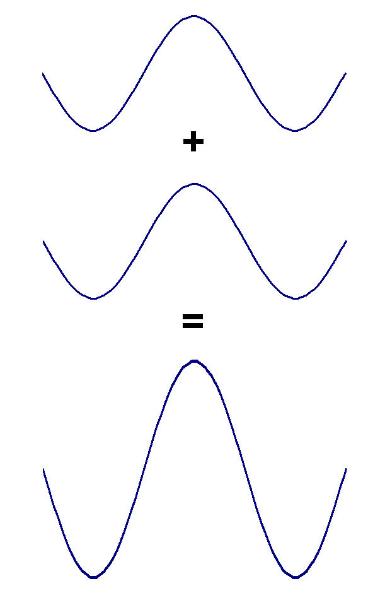
they pass each other and separate again). If we take two simple wave profiles (so called sine waves) as
shown below, and add them together when the two waves overlap in phase, what do we get? By in
phase we mean that the crests of one wave exactly coincide with the crests of the other, as do the
troughs - in other words the waves have identical shape and wavelength and frequency. In this case
they are also of the same height.
Another fundamental property of (most) waves is that waves can be added together or subtracted in a
proportional (or linear) manner. You may have noticed how waves can interfere with one another as
they cross over in a pond, changing shape when they coincide (and returning to their original shape as
they pass each other and separate again). If we take two simple wave profiles (so called sine waves) as
shown below, and add them together when the two waves overlap in phase, what do we get? By in
phase we mean that the crests of one wave exactly coincide with the crests of the other, as do the
troughs - in other words the waves have identical shape and wavelength and frequency. In this case
they are also of the same height.
As you can see, we have ended up with a single wave with twice the height (but the same frequency,
wavelength and basic shape as the two parent waves). When two or more waves interfere so as to
reinforce the disturbance of the water we say that the two waves have interfered constructively.
What we have done is taken each point in space (i.e. from left to right) and added the amplitudes of the
two waves to get the final wave. (Note that if we add a trough then we must take its amplitude to be
negative, whilst the amplitude for a crest is positive - negative amplitudes are downward displacements
of the water surface, whilst positive amplitudes are upward displacements).).
Now, what happens when we add two identical waves which are exactly out of phase, such that the
crests of one coincide with the troughs of the other is shown below:
wavelength and basic shape as the two parent waves). When two or more waves interfere so as to
reinforce the disturbance of the water we say that the two waves have interfered constructively.
What we have done is taken each point in space (i.e. from left to right) and added the amplitudes of the
two waves to get the final wave. (Note that if we add a trough then we must take its amplitude to be
negative, whilst the amplitude for a crest is positive - negative amplitudes are downward displacements
of the water surface, whilst positive amplitudes are upward displacements).).
Now, what happens when we add two identical waves which are exactly out of phase, such that the
crests of one coincide with the troughs of the other is shown below:
As you can see, the two waves have cancelled one another out, they have undergone destructive
interference. We end up with calm water that is undisturbed. Notice, however, that if the waves are
travelling in different directions, then they will return as soon as they separate or the relative phase
changes. Of course, in a real body of water, there may be many different such sine waves adding and
subtracting, each with a different amplitude, frequency and wavelength and speed and direction of
motion. The result can be a very complicated pattern. However, the process is simple at least in
principle - we simply add the waves by adding the amplitude of each at a given point to obtain the
overall displacement of the water at this point. This straight-forward addition of the amplitudes of
waves is called linear addition or linear superposition. (Linear because we don't do anything more
complicated like squaring the amplitudes and then adding them).
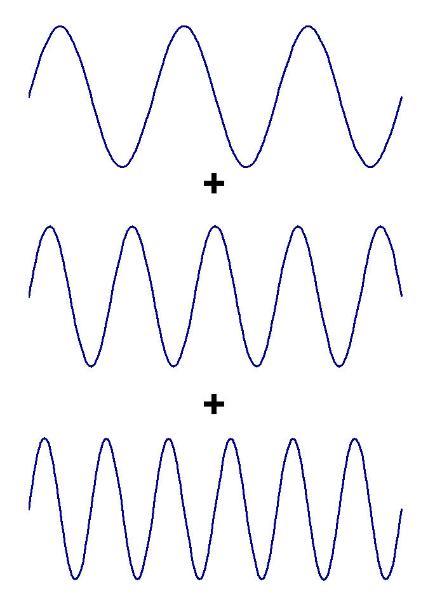
Now let us add three more waves to our original wave and see what happens:
interference. We end up with calm water that is undisturbed. Notice, however, that if the waves are
travelling in different directions, then they will return as soon as they separate or the relative phase
changes. Of course, in a real body of water, there may be many different such sine waves adding and
subtracting, each with a different amplitude, frequency and wavelength and speed and direction of
motion. The result can be a very complicated pattern. However, the process is simple at least in
principle - we simply add the waves by adding the amplitude of each at a given point to obtain the
overall displacement of the water at this point. This straight-forward addition of the amplitudes of
waves is called linear addition or linear superposition. (Linear because we don't do anything more
complicated like squaring the amplitudes and then adding them).
Now let us add three more waves to our original wave and see what happens:
This time we get a much more complicated shape as shown below (this wave is actually sin(x) + sin
(2x) + sin(3x) + sin(4x) for the mathematically minded):
(2x) + sin(3x) + sin(4x) for the mathematically minded):
Refraction
The speed at which a wave travels depends upon the medium (substance) that it travels through as well
as the type of wave. Let's consider light waves as an example. The speed of light in a vacuum is a
constant, c = 2.998 x 10^8 m/s and no ordinary matter can travel faster than this. However, light slows
down in denser media. In air, which is slightly denser than a vacuum, light travels slightly slower than c,
and in glass it travels slower still. The refractive index of a material measures the degree of this
retardation. The refractive index, n, is given by:
n = c / v,
where c is the speed of light in the reference material, usually the vacuum or air, and v is the velocity of
light in the less dense medium. For example, the refractive index of glass is typically around 1.5, for
sapphire, n is about 1.77, cubic zirconia 2.2.
Refraction does more than slowing light down, the light rays also bend when they cross the boundary
between a less dense and more dense material in either direction. For example, when light moves from
air into glass it bends by a certain angle given by the refractive index. This property is used in optics to
focus and defocus light. Examples of this are shown below.
The speed at which a wave travels depends upon the medium (substance) that it travels through as well
as the type of wave. Let's consider light waves as an example. The speed of light in a vacuum is a
constant, c = 2.998 x 10^8 m/s and no ordinary matter can travel faster than this. However, light slows
down in denser media. In air, which is slightly denser than a vacuum, light travels slightly slower than c,
and in glass it travels slower still. The refractive index of a material measures the degree of this
retardation. The refractive index, n, is given by:
n = c / v,
where c is the speed of light in the reference material, usually the vacuum or air, and v is the velocity of
light in the less dense medium. For example, the refractive index of glass is typically around 1.5, for
sapphire, n is about 1.77, cubic zirconia 2.2.
Refraction does more than slowing light down, the light rays also bend when they cross the boundary
between a less dense and more dense material in either direction. For example, when light moves from
air into glass it bends by a certain angle given by the refractive index. This property is used in optics to
focus and defocus light. Examples of this are shown below.




These pictures depict waves spreading
out from a disturbance on the surface
of the water. The two pictures in
grey-scale (above and left) are
computer plots of sine waves. The
simplest waves are sine or cosine
waves in which the surface of the water
undulates up and down according to a
sine wave. Modest single disturbances
can produce similar patterns. In reality
most waves are more complex
combinations of a number of different
sine waves (as is explained below).
out from a disturbance on the surface
of the water. The two pictures in
grey-scale (above and left) are
computer plots of sine waves. The
simplest waves are sine or cosine
waves in which the surface of the water
undulates up and down according to a
sine wave. Modest single disturbances
can produce similar patterns. In reality
most waves are more complex
combinations of a number of different
sine waves (as is explained below).
Above: superposition of two damped
sine waves, one wave is 45 degrees
out of phase with the other, meaning
that both waves have the same
wavelength , but one is one eight of a
wavelength in front of the other (one
wavelength corresponds to an
oscillation or phase angle of 360
degrees).
sine waves, one wave is 45 degrees
out of phase with the other, meaning
that both waves have the same
wavelength , but one is one eight of a
wavelength in front of the other (one
wavelength corresponds to an
oscillation or phase angle of 360
degrees).
Above: Fraunhofer diffraction of light
passing through a narrow circular
aperture and projected onto a screen.
Note that outside the central beam are
concentric rings that rapidly fade in
intensity with radial distance from the
centre of the image. This is a
mathematical plot that makes use of
Bessel's functions.
passing through a narrow circular
aperture and projected onto a screen.
Note that outside the central beam are
concentric rings that rapidly fade in
intensity with radial distance from the
centre of the image. This is a
mathematical plot that makes use of
Bessel's functions.
Above: a damped sine wave fades in
intensity (amplitude) with distance from
the source. This plot is of a sine
function multiplied by an exponential
decay function.
intensity (amplitude) with distance from
the source. This plot is of a sine
function multiplied by an exponential
decay function.
More types of waves
Life is about balance. Without a centre of balance all ordered systems would collapse into chaos.
Buildings would topple, the Sun would either explode or turn cold, your body would combust or enter
torpor, every thing that was in motion would have no particular resting place and no particular path.
When any system that is at rest, such as a spring at its natural length or a pendulum hanging straight
down, is perturbed or moved from this resting or equilibrium position, a restoring force tries to pull it
back. In the spring, this restoring force would be its tension if it was stretched, gravity pulls on the
pendulum bob and on the water in the wave. This compensating force invariable over-compensates - it
pulls the system past its resting point. The water in the crest of the wave plunges forcefully, the spring
springs back with force, as does the string on a guitar, and the pendulum swings past the vertical. So
the system is displaced from its equilibrium again, but on the other side and so again a restoring force
acts to pull it back. This continues as the system is set into oscillation, the spring oscillates, the
pendulum swings, the water in the wave continues moving up and down.
These oscillations or waves characterise all physical systems. Your body temperature oscillates around
the set point of 37 degrees C (albeit by only a fraction of a degree either side), the electrons in atoms
are waves, light is a wave of electromagnetic energy as are radio waves and microwaves, sound is a
wave of air molecule vibration or alternating air pressure, the atoms in a table vibrate as if attached to
one another by springs, and earthquakes are waves of vibration that make the Earth ring like a bell.
Everything is a wave or oscillation. Even moral standards in society oscillate around a set point, from too
severe to too merciful. Shares rise and fall on the stock exchange. Waves of electrical activity pulse
across your brain.
So what disturbs a system from its equilibrium in the first place? The answer is energy, for energy can
produce a force. Electrical power sets electrical charge in motion in an antenna, and this moving electric
charge generates radio waves. You can pull on a spring or push a pendulum to set it in motion. The
wind whips up the water, causing gravity to pull it back down. Without energy, matter would be in a
permanent state of rest. The path of balance is indeed very narrow, so narrow that nothing can remain
in perfect balance. If your body temperature rises to around 40-45 C or higher or drops to 30 C or lower
then you may die. However, body temperature it cannot remain at the optimum of 37 C exactly - one
moment the body generates too much heat and core temperature rises to 37.1 C, this triggers cooling
responses and your heat generation is reduced, but this overcompensates and your temperature may
fall to 36.9 CF, triggering it to warm up again, and so on. The vibrations of a loudspeaker make the air
vibrate, creating sound. Notice that disturbances often spread - set a region of air vibrating and this
triggers the air next to it to vibrate, and so on, as the sound travels through the air.
So what causes the oscillations to stop? If energy could be perfectly converted from gravity to energy of
movement (kinetic energy) and vice versa with 100% efficiency, then our pendulum would oscillate
forever (or until it was forcefully restrained). Such a perpetual motion machine is seemingly
impossible. The reason being that some energy is lost from the system in forms that the system can not
use to continue the oscillations. As the pendulum slices through the air, some energy (given to it
originally by the person who pushed or pulled it) is lost as heat and sound. This causes the system to
eventually wind down or dampen down back to its resting equilibrium. Every machine generates some of
this 'wasted' or 'disordered' energy, usually as heat and sound. This is just as well, otherwise we would
end up in chaos again, with everything whizzing about with no place of rest.
So you see, the study of waves is central to physics. A combination of energy and a restoring 'force'
produces oscillations or waves.
Life is about balance. Without a centre of balance all ordered systems would collapse into chaos.
Buildings would topple, the Sun would either explode or turn cold, your body would combust or enter
torpor, every thing that was in motion would have no particular resting place and no particular path.
When any system that is at rest, such as a spring at its natural length or a pendulum hanging straight
down, is perturbed or moved from this resting or equilibrium position, a restoring force tries to pull it
back. In the spring, this restoring force would be its tension if it was stretched, gravity pulls on the
pendulum bob and on the water in the wave. This compensating force invariable over-compensates - it
pulls the system past its resting point. The water in the crest of the wave plunges forcefully, the spring
springs back with force, as does the string on a guitar, and the pendulum swings past the vertical. So
the system is displaced from its equilibrium again, but on the other side and so again a restoring force
acts to pull it back. This continues as the system is set into oscillation, the spring oscillates, the
pendulum swings, the water in the wave continues moving up and down.
These oscillations or waves characterise all physical systems. Your body temperature oscillates around
the set point of 37 degrees C (albeit by only a fraction of a degree either side), the electrons in atoms
are waves, light is a wave of electromagnetic energy as are radio waves and microwaves, sound is a
wave of air molecule vibration or alternating air pressure, the atoms in a table vibrate as if attached to
one another by springs, and earthquakes are waves of vibration that make the Earth ring like a bell.
Everything is a wave or oscillation. Even moral standards in society oscillate around a set point, from too
severe to too merciful. Shares rise and fall on the stock exchange. Waves of electrical activity pulse
across your brain.
So what disturbs a system from its equilibrium in the first place? The answer is energy, for energy can
produce a force. Electrical power sets electrical charge in motion in an antenna, and this moving electric
charge generates radio waves. You can pull on a spring or push a pendulum to set it in motion. The
wind whips up the water, causing gravity to pull it back down. Without energy, matter would be in a
permanent state of rest. The path of balance is indeed very narrow, so narrow that nothing can remain
in perfect balance. If your body temperature rises to around 40-45 C or higher or drops to 30 C or lower
then you may die. However, body temperature it cannot remain at the optimum of 37 C exactly - one
moment the body generates too much heat and core temperature rises to 37.1 C, this triggers cooling
responses and your heat generation is reduced, but this overcompensates and your temperature may
fall to 36.9 CF, triggering it to warm up again, and so on. The vibrations of a loudspeaker make the air
vibrate, creating sound. Notice that disturbances often spread - set a region of air vibrating and this
triggers the air next to it to vibrate, and so on, as the sound travels through the air.
So what causes the oscillations to stop? If energy could be perfectly converted from gravity to energy of
movement (kinetic energy) and vice versa with 100% efficiency, then our pendulum would oscillate
forever (or until it was forcefully restrained). Such a perpetual motion machine is seemingly
impossible. The reason being that some energy is lost from the system in forms that the system can not
use to continue the oscillations. As the pendulum slices through the air, some energy (given to it
originally by the person who pushed or pulled it) is lost as heat and sound. This causes the system to
eventually wind down or dampen down back to its resting equilibrium. Every machine generates some of
this 'wasted' or 'disordered' energy, usually as heat and sound. This is just as well, otherwise we would
end up in chaos again, with everything whizzing about with no place of rest.
So you see, the study of waves is central to physics. A combination of energy and a restoring 'force'
produces oscillations or waves.
Above: Pov-Ray is capable of modelling refraction. Here we have added tiny particles (such as dust,
smoke or air) in the path of the light beam to make it visible - when you shine a torch it is the scattering
(i.e. bouncing off) of light from air and particles in the air that allows you to see the beam side-on, as
this scattering throws a small portion of the light out from the beam in all directions. (Otherwise you
would only see the beam when you look directly into it or when it reflects off a target). On the left a
biconcave diverging lens (n = 1.5) spreads the beam out, and on the right a biconvex lens of the same
material focuses the beam into a point on the screen. (The slight distortions in the beams, especially
the divergent beam, appear to be caused by light reflecting off the screen and scattering off the
particles).
smoke or air) in the path of the light beam to make it visible - when you shine a torch it is the scattering
(i.e. bouncing off) of light from air and particles in the air that allows you to see the beam side-on, as
this scattering throws a small portion of the light out from the beam in all directions. (Otherwise you
would only see the beam when you look directly into it or when it reflects off a target). On the left a
biconcave diverging lens (n = 1.5) spreads the beam out, and on the right a biconvex lens of the same
material focuses the beam into a point on the screen. (The slight distortions in the beams, especially
the divergent beam, appear to be caused by light reflecting off the screen and scattering off the
particles).
Above: on the right of each image is a converging lens, as seen from behind. A beam of light strikes
each lens from behind and we look toward the screen. In the leftmost image refraction is turned off and
all we see is a dimming of the light as it passes through the translucent lens. When we turn refraction on
the next image, with n = 1.10, light passing through the lens is focused onto a smaller area, causing it to
brighten and leaving a dark area where no light hits the screen (because it has been focused into the
bright central circle). Note there is no air or smoke here to scatter the beam, so the beam itself is
invisible. The pink area is unfocused light that passes outside the lens, since here we used a diverging
cone of light, rather than a narrow beam, and this shows us the background light intensity, which is quite
dim and so appears less white than the focused beam. In the third image, n = 1.15 and so the light
bends more and focuses more - the lens is stronger. Making the lens thicker achieves the same result.
On the right, n = 2.00, and so the light is focused very strongly into a small spot.
each lens from behind and we look toward the screen. In the leftmost image refraction is turned off and
all we see is a dimming of the light as it passes through the translucent lens. When we turn refraction on
the next image, with n = 1.10, light passing through the lens is focused onto a smaller area, causing it to
brighten and leaving a dark area where no light hits the screen (because it has been focused into the
bright central circle). Note there is no air or smoke here to scatter the beam, so the beam itself is
invisible. The pink area is unfocused light that passes outside the lens, since here we used a diverging
cone of light, rather than a narrow beam, and this shows us the background light intensity, which is quite
dim and so appears less white than the focused beam. In the third image, n = 1.15 and so the light
bends more and focuses more - the lens is stronger. Making the lens thicker achieves the same result.
On the right, n = 2.00, and so the light is focused very strongly into a small spot.
Left: the experimental set-up used in these experiments - a light source with
an adjustable aperture and which switch between a narrow beam or a
spreading cone of light of any colour and intensity, shines light through a
lens and projects the focused light onto a screen.
an adjustable aperture and which switch between a narrow beam or a
spreading cone of light of any colour and intensity, shines light through a
lens and projects the focused light onto a screen.
Above and below: if we use a spherical lens (a flattened sphere) then the light is not focused very
clearly and pronounced spherical aberration occurs, creating rings of light around the central image.
clearly and pronounced spherical aberration occurs, creating rings of light around the central image.
Left: a common example of refraction - the straw appears
to bend in the water and appears off-set and slightly
thicker. Reflection of the straw in the surface of the water
and the bottom of the glass can also be seen.
to bend in the water and appears off-set and slightly
thicker. Reflection of the straw in the surface of the water
and the bottom of the glass can also be seen.
Notice how we have some small crests and fewer large crests repeating in a periodic fashion. In fact, if
we added an infinite number of waves together (that is add sin(nx) for n= 1,2,3, ... ) or at least a very
large number, we can generate a single large crest and no other crests or troughs - a pulse rather
than a wave. This type of wave is called a soliton (solitary pulse). Solitons can occur in nature, an
example being river bores. In tidal rivers (those with estuaries subject to tidal influences) then a soliton
will travel up the river (against the flow!) at periodic intervals linked to the tides, such a soliton is called
a river bore, for example the Severn bore which travels up the river Severn in England.
Reflection
When a wave, such as light strikes a smooth reflective surface, the light rays bounce off at an equal
and opposite angle to the angle of the incoming (incident) beam. Pov_Ray can simulate this reflection
for us, as shown below:
we added an infinite number of waves together (that is add sin(nx) for n= 1,2,3, ... ) or at least a very
large number, we can generate a single large crest and no other crests or troughs - a pulse rather
than a wave. This type of wave is called a soliton (solitary pulse). Solitons can occur in nature, an
example being river bores. In tidal rivers (those with estuaries subject to tidal influences) then a soliton
will travel up the river (against the flow!) at periodic intervals linked to the tides, such a soliton is called
a river bore, for example the Severn bore which travels up the river Severn in England.
Reflection
When a wave, such as light strikes a smooth reflective surface, the light rays bounce off at an equal
and opposite angle to the angle of the incoming (incident) beam. Pov_Ray can simulate this reflection
for us, as shown below:
Dispersion
In real materials light of different wavelengths (colours) is refracted or bent to a different degree. This
can cause the individual colours of the spectrum that make up white light to spread-out and separate -
in other words to disperse. With a focusing lens this effect causes some chromatic aberration that sets
up colour fringes around the image, but the effect is much more dramatic if a prism is used, since the
prism will refract the light in one direction, dispersing the colours along a line which makes them easy
to see. This can be seen in the Pov-Ray simulation below:
In real materials light of different wavelengths (colours) is refracted or bent to a different degree. This
can cause the individual colours of the spectrum that make up white light to spread-out and separate -
in other words to disperse. With a focusing lens this effect causes some chromatic aberration that sets
up colour fringes around the image, but the effect is much more dramatic if a prism is used, since the
prism will refract the light in one direction, dispersing the colours along a line which makes them easy
to see. This can be seen in the Pov-Ray simulation below:
Above: a Pov-Ray simulation of a light beam reflecting off a smooth mirror. Smoke particles
have been added to the path of the beam to make it visible.
have been added to the path of the beam to make it visible.
Above left: light striking the edge of the mirror gets
reflected in two opposite directions.
reflected in two opposite directions.
Above: a half-cube will reflect the light back at
us! (Note: refraction has been turned off in
this image). A corner cube is a pyramidal
piece of glass which will do this no matter what
direction the incident beam strikes it from.
us! (Note: refraction has been turned off in
this image). A corner cube is a pyramidal
piece of glass which will do this no matter what
direction the incident beam strikes it from.
Radio waves, like visible light, are also waves of electromagnetic energy and they can be reflected. A
satellite dish is shaped like a parabola which has the property of reflecting the waves onto the same
target spot at the tip of the antenna projecting from the centre of the dish. In this way a parabolic
reflector acts as a lens and focuses the rays. Similarly, parabolic reflectors in car and torch lamps, and
in the light-producing organs (photophores) of certain squid and fish, are also parabolic and reflect a
focused beam of light. Water waves can also be seen to bounce off rocks and sea walls. Sound waves
will bounce off buildings and other obstacles, etc. etc.
satellite dish is shaped like a parabola which has the property of reflecting the waves onto the same
target spot at the tip of the antenna projecting from the centre of the dish. In this way a parabolic
reflector acts as a lens and focuses the rays. Similarly, parabolic reflectors in car and torch lamps, and
in the light-producing organs (photophores) of certain squid and fish, are also parabolic and reflect a
focused beam of light. Water waves can also be seen to bounce off rocks and sea walls. Sound waves
will bounce off buildings and other obstacles, etc. etc.
Article updated:
28 March 2016
28 March 2016































